- Müəllif admin carl@lifeloveeveryday.com.
- Public 2023-12-16 19:16.
- Son dəyişdirildi 2025-01-23 15:28.

Qızıl Nisbət nümunələrinə klassik memarlıqda, incəsənətdə, təbiətdə və hətta musiqidə hər yerdə rast gəlmək olar. İlahi Nisbət kimi də tanınan bu nisbət ifadəsi həm təbii, həm də insan istehsalı olan dizaynda irrasional ədədin (1.618) tətbiqi ilə ahəngdar kompozisiya təklif edir. Çox güman ki, siz Qızıl Nisbətin gözəlliyinin arxasında duran riyaziyyatdan xəbərsizsiniz, çünki o, heç bir izahata ehtiyac duymadan təbii olaraq xoşunuza gələcək əşyalar və musiqilər yaradır.
Memarlıqda Qızıl Nisbət
Qızıl Nisbət təbiətdə və sənətdə demək olar ki, mükəmməl gözəllik yaradır. Gündəlik həyatda Qızıl Nisbət nümunələri axtarmağa başladığınız zaman, bir çox monumental bina və tikililər yaratmaq üçün istifadə edildiyi bir çox nümunəyə təəccüblənə bilərsiniz. Qızıl nisbət memarlıqda istifadə edildikdə, binanın "müqəddəs memarlıq" istifadə edilərək yaradıldığı deyilir. Memarlar və dizaynerlər Qızıl Nisbət hesablamasını kvadrata tətbiq etməklə, insan gözünə estetik baxımdan ən gözəl nisbətlərə sahib olduğuna inanılan Qızıl Düzbucaqlı yarada bilirlər.
Qızıl Düzbucaqlı Nümunə: Parthenon

Yunan heykəltəraşı Phidias, xüsusilə Parthenon sütunlarının bir qədər yuxarısında heykəl qoyduğu bantlarla işləməyə başladığı zaman, işində Qızıl Nisbətdən istifadə etdi. Onu da qeyd etmək lazımdır ki, Qızıl Nisbətə təyin edilmiş rəqəmsal dəyər, Phi onun şərəfinə adlandırılıb.
Parthenonun xarici görünüşünün ölçülərini ölçsəniz, onun təkcə Qızıl Düzbucaqlı əmələ gətirmədiyini, həm də sütunlar arasında çoxlu Qızıl Düzbucaqlıların olduğunu kəşf edəcəksiniz. Bu müqəddəs tikili memarlıqda Qızıl Nisbətin gözəl nümunəsidir.
Qızıl Üçbucaq Nümunə: Böyük Giza Piramidası
Qızıl Nisbət, Qızıl Düzbucaqlı və Qızıl Üçbucaq dünyanın Yeddi Möcüzəsindən biri olan Böyük Giza Piramidasının mükəmməlliyində tapıla bilər. Qızıl nisbəti tapmaq üçün piramidanın kvadrat əsasını yarıya endirməli və piramidanın mərkəzinə qədər şaquli xətt çəkməlisiniz. Bu, piramidanın bucaqlı tərəfinə birləşdirildikdə, onun Qızıl Nisbət olan 1,618 nisbətli Qızıl Üçbucağı necə əmələ gətirdiyini asanlıqla görə bilərsiniz.
Digər Memarlıq Nümunələri
Qədimdən müasir müqəddəs memarlıq və Qızıl Nisbət binalarının bir çox nümunəsini tapa bilərsiniz.
- Chartres Katedrali - Mərkəz, Fransa
- Notre Dame - Paris, Fransa
- Qızlar eyvanı - Akropol, Afina
- Tac Mahal - Aqra, Hindistan
- Birləşmiş Millətlər Binası - Nyu York, Nyu York
Sənət Nümunələrində Qızıl Nisbət
Qızıl Nisbətdən istifadə edən usta rəssamların çoxlu nümunələrinə rast gələ bilərsiniz. Bu mükəmməllik əsərləri Qızıl Düzbucaqlılar və Qızıl Üçbucaqlar nisbətindən istifadə etməklə yaradılmışdır. Qızıl Dördbucaq əsasında yaradılmış incəsənət insan gözünü daha çox sevindirir. Bu mükəmməl düzbucaqlı və Qızıl Nisbəti əhatə edən sirrlərdən biridir.
Sənətdə Qızıl Nisbət

Qızıl nisbət sənət nümunələrinə aşağıdakılar daxildir:
- Leonardo Di Vinci - Mona Liza, Vitruvian Adam
- Botticelli - Veneranın Doğulması
- Mikelancelo - Müqəddəs Ailə, 'David'
- Rafael - Çarmıxa çəkilmə
- Rembrandt - Avtoportret
- Salvador Dali - Son Şam yeməyinin müqəddəs mərasimi, Yaddaşın davamlılığı
Bədii Kompozisiyada Qızıl Nisbətdən İstifadə
Qızıl Düzbucaqlının daxilində digər sahələrə nisbətən vizual olaraq daha cəlbedici olan müəyyən sahələr var. Bu nöqtələr düzbucaqlının aşağı küncündən əks küncə doğru xətt çəkmək və onu digər alt künc ilə təkrarlamaqla aşkar edilir. Bu xətlər Qızıl Düzbucağın tam mərkəzində kəsişəcək. Sonra, mərkəz nöqtəsindən başlayaraq hər bir xətt boyunca orta yolu ölçün. Bu dörd nöqtə düzbucağın gözləri adlanır (Qızıl Nisbət). Rəsmin əsas mərkəz nöqtəsi daha sonra bu maraq nöqtələri (nisbətləri) daxilində çəkilir və ya rənglənir.
Musiqidə Qızıl Nisbət

Musiqi ədədi dəyərdən ibarətdir və musiqi əsəri yaratmaq üçün Qızıl Nisbətdən istifadə edildikdə, riyaziyyatın canlı nümunəsinə çevrilir. Fibonacci Sequence musiqidə də üstünlük təşkil edir:
- Tərəzidə səkkiz not var.
- Üçüncü və beşinci notlar akkordların əsasını təşkil edir.
- Hər hansı bir notun uzunluğu və ya oktavası 13 notdur.
Ardıcıllıq musiqi parçası boyu davam edir və Qızıl Nisbətə çatdıqca daha mürəkkəbləşir.
Qızıl nisbətdən istifadə edən bəstəkarlar
Ən məşhur klassik bəstəkarlardan bəziləri Bax, Bethoven, Şopen və Motsart da daxil olmaqla, öz musiqi əsərlərində Qızıl nisbət və Fibonaççi ardıcıllığından istifadə etmişlər. Keysi Monqoven kimi bəzi müasir bəstəkarlar musiqilərində Qızıl Nisbəti tədqiq ediblər.
Təbiətdəki Qızıl Nisbət Nümunələri

Təbiətdə Qızıl Nisbət haradadır? Qızıl nisbətdən istifadə etməklə yaradıla bilən Qızıl və ya Fibonaççi Spiralındadır. Bu, təbiət aləmində çox rast gəlinən bir fenomendir. Bitkinin yarpaqları o qədər böyüyərsə, gövdəni yuxarı qaldıra bilər. Yeni yarpaq yalnız onun əmələ gəlməsinə davam edən yarpaqdan sonra əmələ gəlir.
- Spiral kaktuslar
- Spiral qalaktikalar
- Günəbaxan
Fibonacci ardıcıllığı ilə çiçəklər
Bəzi çiçəklərin Fibonaççi ardıcıllığına əməl edən çiçək ləçəkləri var:
- Üç ləçək:İris, zanbaq, orkide, trillium
- Beş ləçək: Buttercups, ətirşah, hibiskus, səhər şöhrəti, nasturtium
- Səkkiz ləçək: Delphiniums
- 13 ləçək: Bəzi növ papatyalar, ragwort, marigold
Şam qozalarında Fibonacci Spiral

Ağac növündən asılı olaraq, şam qozalarında Fibonacci sayı seriyası daxilində Qızıl Nisbəti də görə bilərsiniz. Şam ağacının bir tərəfində bir sıra səkkiz spiral, digər tərəfində isə 13 spiral tapa bilərsiniz. Başqa bir şam qozu naxışının bir tərəfində səkkiz, digər tərəfində isə beş spiral var.
İnsanlarda Qızıl Nisbət
Bu nisbət təkcə insanların bir-birlərinə necə baxdıqları üçün deyil, həm də bədənlərinin necə işlədiyi və DNT-si baxımından da vacibdir.
DNT Qızıl Nisbəti Göstərir
Qızıl Nisbətin ən heyrətamiz nümunələrindən biri insan DNT strukturundadır. Bu, DNT cüt spiralının onbucaqlı formasını meydana gətirdiyini göstərən tək bir DNT kəsiyində görülə bilər. Bu, bir-birindən 36 dərəcə fırlanan iki beşbucağın birləşməsidir və DNT cüt spiralını əmələ gətirir. İkiqat spiral spiral özü beşbucaqlı əmələ gətirir. Hətta tək bir DNT molekulu belə Qızıl Bölmənin və ya İlahi nisbətin əsasını ortaya qoyur.
Qızıl Nisbətin Arxasındakı Riyaziyyat
Real həyatda Qızıl Nisbəti tapmaq hər yerdə göründüyü kimi sadədir. Bu, əsrlər boyu insanlar tərəfindən təkrarlanan və təqlid edilən təbiətdə tapılan mükəmməl rəqəm kimi tanınanı müəyyən etmək üçün istifadə olunan riyazi bir həqiqətdir. Bu nömrənin sadə gözəlliyi onun icradakı mürəkkəbliyini gizlədir. Qızıl Nisbətin arxasında duran nəzəriyyəni başa düşmək üçün əvvəlcə nisbətin Fibonaççi ardıcıllığını araşdırmaq lazımdır.
Fibonacci Ardıcıllığı və Qızıl Nisbət
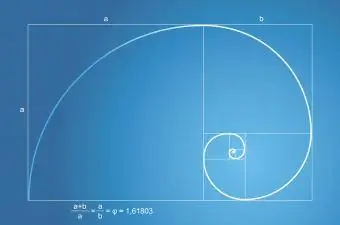
Fibonacci Sequence və ya Seriyasının Qızıl Nisbətlə əlaqəsi var. Fibonacci seriyası bitkidəki yarpaqların və çiçəkdəki ləçəklərin sayında özünü göstərir. Təbiətdə rast gəlinən Fibonaççi spirali həmişə Qızıl Nisbəti olan Qızıl Düzbucaqlının bir hissəsidir.
Fibonacci Seriyası riyaziyyatı sadədir:
- Ardıcıllıq 0 və 1 ilə başlayır.
- Serialdakı növbəti nömrəni əldə etmək üçün sadəcə son iki rəqəmi əlavə edin.
- 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8 və s.
- Bu Fibonacci Seriyasının nümunəsi belə olur: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 və s.
Fibonacci-nin Qızıl Nisbətlə əlaqəsi, irəli, irəli və daha irəli əlavə edildikdə həyata keçirilir. Serialı nə qədər çox əlavə etsəniz, Qızıl Nisbətə bir o qədər yaxınlaşırsınız.
Qızıl düzbucaqlı və üçbucaq yaratmaq
Fibonaççi ardıcıllığı ilə Qızıl Düzbucaqlı yaratmaq üçün kvadratdan başlayırsınız. Orijinal kvadrata başqa bir kvadrat əlavə edərək düzbucaqlı qurmağa başlayacaqsınız. Formuladan istifadə etməyi unutmayın: 0+1=1 birinci kvadratdır, 1+1=2 - başqa kvadrat əlavə edəcəksiniz.1+2=3 üç kvadrat əlavə edəcəksiniz və növbəti, 2+3=5, beş kvadrat əlavə edəcəksiniz. Siz kvadratlar əlavə etməyə və nəticədə Qızıl Düzbucaq yaratmağa davam edəcəksiniz.
Qızıl Üçbucaq Qızıl Düzbucağı bir küncdən qarşı küncə ikiyə bölməklə yaradıla bilər. Bu, üç tərəfinin və ya bucağının 2:2:1 nisbətinə malik olduğu üçbucaq yaradır, yəni iki uzun tərəf bərabər uzunluqdadır və qısa bucaq iki daha uzun tərəfin tam yarısı qədərdir.
Real Dünyada Qızıl Nisbət
Qızıl Nisbət təbiətdə və insan bədənində ön plana çıxdığına görə tez-tez İlahi Nisbət adlandırılır. Qızıl Nisbətin bir çox canlıda mövcud olmasının kəşfi bu sehrli nisbətə olan hörməti gücləndirdi və bu gün rəssamlar və yaradıcılar üçün ilham mənbəyi olmaqda davam edir.






